Задача. Числа Фібоначчі.
Задача. Числа Фібоначчі.
Алгоритм
утворення чисел Фібоначчі мовою Паскаль
Program
Fibonachi_1; {Рекурсивна форма}
Var N:Integer;
A:Array[1..46] of LongInt;
Function
Fibo(X:Integer):LongInt;
Begin if A[X]=0 then if
(X=1) or (X=2) then A[X]:=1
else
A[X]:=Fibo(X-1)+Fibo(X-2); Fibo:=A[X];
end; {End Fibo}
begin write('Введіть N:'); readln(N);
writeln(Fibo(N)); end.
Завдання для самостійного програмування.
1.
Записати алгоритм, який знаходить суму чисел
Фібоначчі і їх кількість, що менші натурального числа N.
2.
Записати алгоритм, який знаходить суму парних
чисел Фібоначчі і їх кількість, що менші
натурального числа N.
3.
Записати алгоритм, який знаходить суму простих чисел
Фібоначчі і їх кількість, що менші
натурального числа N.
4.
Записати алгоритм, який знаходить числа
Фібоначчі і їх кількість, що діляться
націло на 3 і менші натурального числа N.
5.
Записати алгоритм, який знаходить числа
Фібоначчі, що діляться націло на 5 і на
2 їх кількість, які менші натурального числа N.
теорія
рекурентним співвідношенням другого порядку
і т. д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях — комбінаторних, числових, геометричних.
В природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 — у дуба, 3/8 — у тополі і груші, 5/13 — у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.
Зміст
[сховати]Формула Біне[ред. • ред. код]
Числа Фібоначчі тісно пов'язані з золотим перетином 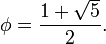 Формула Біне виражає за допомогою
Формула Біне виражає за допомогою  значення
значення 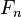 в явному вигляді як функцію від
в явному вигляді як функцію від  :
:
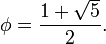 Формула Біне виражає за допомогою
Формула Біне виражає за допомогою  значення
значення 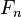 в явному вигляді як функцію від
в явному вигляді як функцію від  :
:
При цьому 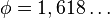 і
і 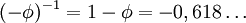 є коренями квадратного рівняння
є коренями квадратного рівняння 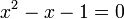 .
.
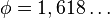 і
і 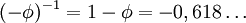 є коренями квадратного рівняння
є коренями квадратного рівняння 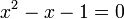 .
.
Оскільки 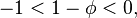 знаходимо, що при
знаходимо, що при 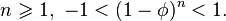 Тому з формули Біне випливає, що для всіх натуральних
Тому з формули Біне випливає, що для всіх натуральних 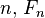 є найближчим до
є найближчим до 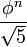 цілим числом, тому
цілим числом, тому ![F_n = \left[\frac{\phi^n}{\sqrt{5}}\right]](http://upload.wikimedia.org/math/6/7/3/673434bd84a17c7c9bb69b77cde1779f.png) або
або 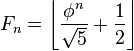 . Зокрема, справедливаасимптотика
. Зокрема, справедливаасимптотика 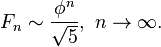
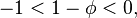 знаходимо, що при
знаходимо, що при 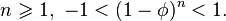 Тому з формули Біне випливає, що для всіх натуральних
Тому з формули Біне випливає, що для всіх натуральних 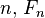 є найближчим до
є найближчим до 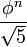 цілим числом, тому
цілим числом, тому ![F_n = \left[\frac{\phi^n}{\sqrt{5}}\right]](http://upload.wikimedia.org/math/6/7/3/673434bd84a17c7c9bb69b77cde1779f.png) або
або 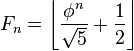 . Зокрема, справедливаасимптотика
. Зокрема, справедливаасимптотика 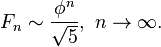
Властивості чисел Фібоначчі[ред. • ред. код]
- Найбільший спільний дільник двох чисел Фібоначчі дорівнює числу Фібоначчі з індексом, рівним найбільшому спільному дільнику індексів, тобто:
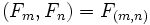 . Внаслідок цього:
. Внаслідок цього: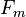 ділиться
ділиться 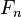 тоді й тільки тоді, коли
тоді й тільки тоді, коли  ділиться на
ділиться на  (за винятком
(за винятком  );
);- кожне третє число Фібоначчі парне (
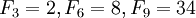 );
); - кожне четверте ділиться на три (
 );
); - кожне п'ятнадцяте закінчується нулем (
 );
); - два сусідніх числа Фібоначчі взаємно прості;
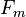 може бути простим тільки для простих
може бути простим тільки для простих  (за єдиним винятком
(за єдиним винятком 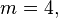 що пов'язано з
що пов'язано з  ). Зворотне твердженняневірне:
). Зворотне твердженняневірне: 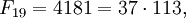 хоча
хоча 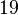 — просте число. Тепер невідомо, чи існує нескінченно багато простих чисел Фібоначчі.
— просте число. Тепер невідомо, чи існує нескінченно багато простих чисел Фібоначчі.
- Використовуючи те саме рекурентне співвідношення, що і на початку, у вигляді
 , можливо поширити визначення чисел Фібоначчі і на від'ємні індекси:
, можливо поширити визначення чисел Фібоначчі і на від'ємні індекси: 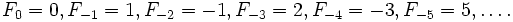 Неважко переконатися, що
Неважко переконатися, що 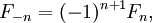 тобто одержуємо таку саму послідовність із знаками, що чергуються.
тобто одержуємо таку саму послідовність із знаками, що чергуються. - Послідовність чисел Фібоначчі є частковим випадком генерованої послідовності, її характеристичний многочлен рівний
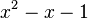 й має корені
й має корені  і
і 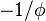 .
. - Генератрисою послідовності чисел Фібоначчі є:
- Числа Фібоначчі можна представити значеннями континуант на наборі одиниць:
 , тобто
, тобто
-
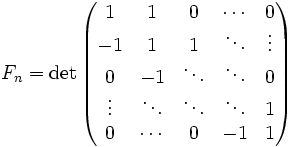 , а також
, а також  ,
,
- де матриці мають розмір
 ,
,  — уявна одиниця.
— уявна одиниця.
- Для будь-якого n,
-
- Ця формула надає швидкий алгоритм обчислення чисел Фібоначчі за допомогою матричного варіанта алгоритма швидкого піднесення до степеня. Обчислення визначників дає:
-
- Відношення
 є підходящими дробами золотого перетину
є підходящими дробами золотого перетину  і, зокрема,
і, зокрема, 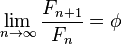 .
. - Суми біноміальних коефіцієнтів на діагоналях трикутника Паскаля є числами Фібоначчі з огляду на формулу
 .
.
- У 1964 р. J. H. E. Cohn довів, що єдиними точними квадратами серед чисел Фібоначчі є
 і
і 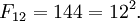
- Множина чисел Фібоначчі збігається з множиною натуральних значень наступного полінома двох змінних
де 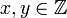 — цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.
— цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.
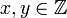 — цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.
— цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.Числа Фібоначчі за logN[ред. • ред. код]
Ідея полягає в наступному.
F_n = F_(n-1) + F_(n-2) F_(n+1) = F_n + F_(n-1) = 2*F_(n-1) + F_(n-2)
Можна користуватися цими формулами в початковому вигляді, проте більш раціонально буде наступне матричне рівняння:
| F_n | | 1 1 | | F_(n-2)| | | = | | | | | F_(n+1)| | 1 2 | | F_(n-1)|.
Якщо через A позначити матрицю
| 1 1 |
A = | |
| 1 2 |,
то отримаєм
| F_(2n) | | 1 | | | = A^n * | | | F_(2n+1)| | 1 |.
Отже, щоб вирахувати 2n-е/2n +1- е число Фібоначчі, треба матрицю A піднести до n-ого степеня, а це можна зробити за O (log n)операцій.
Історія відкриття[ред. • ред. код]
У XIII столітті італійський математик Фібоначчі розв'язував таку задачу:
Фермер годує кроликів. Кожен кролик народжує одного кролика, коли йому стає 2 місяці, а потім дає потомство в 1 кролик кожен місяць. Скільки кроликів буде у фермера через n місяців, якщо спочатку у нього був лише один (вважаємо, що кролики не гинуть і кожен народжений дає потомство за вище описаною схемою)?
Очевидно, що першого та другого місяця у фермера залишається один кролик, оскільки потомства ще немає. На третій місяць буде два кролики, оскільки перший через два місяці народить другого кролика. На четвертий місяць перший кролик дасть ще одного, а другий кролик потомства не дасть, оскільки йому ще тільки один місяць. Отже на четвертий місяць буде три кролики.
Можна помітити, що кількість кроликів після n — го місяця дорівнює кількості кроликів, які були у n — 1 місяці плюс кількість народжених кроликів. Останніх буде стільки, скільки є кроликів що дають потомство, або дорівнює кількості кроликів, яким вже виповнилося 2 місяці (тобто кількості кроликів після n — 2 місяця).
Якщо через Fn позначити кількість кроликів після n — го місяця, то має місце наступне рекурентне співвідношення:
Fn = Fn-1 + Fn-2, F1 = F2 = 1
Покладемо F0 = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … ,
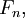
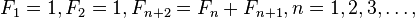
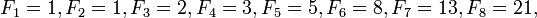

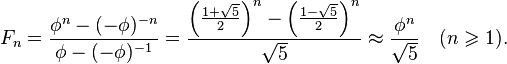
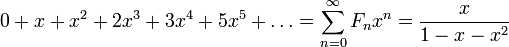
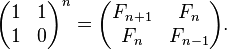
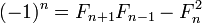

Немає коментарів:
Дописати коментар